Microsoft Power BI
What is Microsoft Power BI?
Microsoft Power BI is a business intelligence (BI) platform that provides nontechnical business users with tools for aggregating, analyzing, visualizing and sharing data. Power BI's user interface is fairly intuitive for users familiar with Excel, and its deep integration with other Microsoft products makes it a versatile self-service tool that requires little upfront training.
Users can download Power BI for Windows 10 or Windows 11, called Power BI Desktop, and native mobile apps for Windows, Android and Apple iOS devices. There is also Power BI Report Server for companies that must maintain their data and reports on premises. That version of Power BI requires a special version of the desktop app -- aptly called Power BI Desktop for Power BI Report Server.
Why is Microsoft Power BI popular?
A few factors make Power BI stand out as an option for businesses requiring BI capabilities. Power BI provides compelling and customizable visuals and requires little in the way of prior analytics or software experience. Many, if not all departments in an organization can use its capabilities, which include these popular ones:
- Usability. Power BI's user-friendly interface and navigation mean it has a simple learning curve for nontechnical business users, who are empowered to create data visuals with a few clicks and no programming experience.
- Affordability. Power BI is offered through different pricing plans so companies of all sizes can take advantage of its capabilities without worrying too much about budgetary constraints.
- Visualizations. Business leaders make use of data storytelling and visually enticing displays that help them communicate with clients, employees and other stakeholders.
- Customization and interactivity. Power BI lets users customize and interact with graphs, charts and other visualizations displaying their data. These features are useful in a number of ways to many different users.
What is Power BI used for?
Microsoft Power BI is used to find insights within an organization's data. It can help connect disparate data sets, transform and clean the data into a data model and create charts or graphs to provide visuals of the data. All of this can be shared with other Power BI users within the organization.
Data models created from Power BI can be used in several ways, including the following:
- Telling stories through charts and data visualizations.
- Examining what-if scenarios within the data.
- Creating reports that answer questions in real time and help with forecasting to make sure departments meet business metrics.
Power BI also provides executive dashboards for administrators and managers, giving management more insight into how departments are doing.
Who uses Power BI?
Power BI is a self-service BI tool that brings data analytics to employees. However, it's mostly data analysts and BI professionals who use it to create the data models before disseminating reports throughout the organization. However, those without an analytical background can still navigate Power BI and create reports.
Both department staff members and management use Power BI to create reports and forecasts to aid sales and marketing reps. They also use it to provide data for management on how a department or individual employees are progressing toward their goals.
In addition, Power BI offers an administrative portal for administrators to configure the implementation of the tool. They can also use the portal to monitor use and manage licenses.
What are the advantages of Power BI?
Multiple advantages make Power BI an attractive option for businesses looking to explore their data through BI visualizations, patterns and insights. These include the following:
- Accessibility. Both nontechnical and technical audiences can easily use Power BI. Its range of pricing options makes it available to businesses with smaller budgets as well as larger enterprises.
- Integrations. Power BI's ability to integrate with software such as Excel and other Microsoft applications means it can work with data from various sources.
- Customer support. Microsoft offers customer support for those in need of troubleshooting and assistance.
- Customization. The ability to create custom visuals adds value for businesses looking to capture and visualize important relationships or patterns found in complex data sets.
- Collaboration. Power BI is built to facilitate collaboration, for example, among different teams within an organization.
- Scalability. Power BI can support large-scale data sets, making it suitable for enterprises as well as small businesses.
What are the disadvantages of Power BI?
While the benefits of the platform appear enticing, there are nonetheless caveats for business users to be aware of, as there are no perfect BI tools in existence yet. They include the following:
- Pricing tiers. While the free, Pro and Premium plans offer the essential capabilities for data reporting and analytics, the free version has a minimum number of features.
- Resource-intensive. Running the platform using an organization's existing infrastructure can consume compute and other resources faster than some organizations can tolerate.
- Dense or cluttered user interfaces. User-friendliness doesn't necessarily equate to neat dashboards as there are many visual components that appear cluttered.
- Vast amounts of features. Analytics and reporting can be done with easy-to-use basic features, but Power BI offers quite a few other features that are more complicated. For example, application programming interfaces (APIs) require complex knowledge and technical expertise.
- Complex table relationships. Power BI can take a few data tables and quickly find relationships among data points, but introducing more tables increases the risk of inaccuracies and slow processing times.
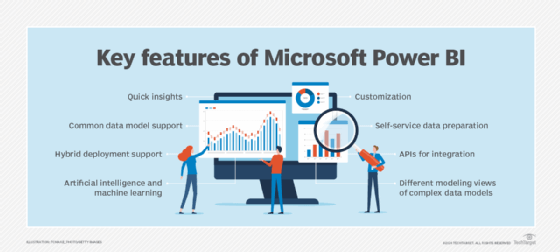
What are key features of Power BI?
Microsoft has added several data analytics features to Power BI since its inception and continues to do so. Some of the most important features include the following:
- Artificial intelligence. Users can access AI-powered image recognition and text analytics in Power BI. They can also create machine learning models using automated capabilities and integrate with Azure Machine Learning. Power BI's Q&A functionality allows users to ask questions and receive responses about data through natural language processing, a branch of AI associated with chatbots. Also, Microsoft is in the process of integrating Copilot, its AI-powered chatbot, into Power BI, giving users the ability to ask questions about data and create custom reports.
- Hybrid deployment support. This feature provides built-in connectors that allow Power BI tools to connect with a number of different data sources from Microsoft, Salesforce and other vendors.
- Quick Insights. This feature allows users to create subsets of data and automatically apply analytics to that information.
- Common data model support. Support for the common data model lets Power BI use a standardized and extensible collection of data schemas, including entities, attributes and relationships.
- Customization. This feature allows developers to change the appearance of default visualization and reporting tools and import new tools into the platform.
- APIs for integration. Developers use sample code and APIs to embed the Power BI dashboard in other software products.
- Self-service data prep. Using Power Query, business analysts can ingest, transform, integrate and enrich big data into the Power BI web service. Ingested data can be shared across multiple Power BI models, reports and dashboards.
- Modeling view. Users can divide complex data models by subject area into separate diagrams, select multiple objects, set common properties, view and modify properties in the properties pane, and set display folders for simpler consumption of complex data models.
Microsoft Power BI update timeline
Power BI initially began as a Microsoft project under a different name and later released as its own platform offering. Significant developments have occurred since its inception. A full timeline includes the following developments:
- 2011. Power BI was originally called Project Crescent and was initially available in July 2011, bundled with Microsoft SQL Server, code name Denali.
- 2013. It was renamed and unveiled in September 2013 as Power BI for Office 365 -- now Microsoft 365.
- 2015. Initially based off Excel features like Power Query, Power Pivot and Power View, Microsoft added features over time, including enterprise-level data connectivity and security options. Power BI was released as a standalone product in July 2015.
- 2017. The Microsoft Power BI desktop app was released in the Windows store.
- 2019. Power AI released AI-based enhancements and previewed Key Influencers, its first AI-powered visualization feature.
- 2020. Power BI Desktop users could access AI insights through Power Query.
- 2023. Microsoft announced generative AI features for Power BI through integration with Microsoft's Copilot.
Microsoft regularly updates the Power BI application with new features and improvements. To get updates, users can download the latest edition from the Power BI site; Microsoft Windows 10 and Windows 11 users can get Power BI Desktop from the Windows Store.
Power BI components
Microsoft Power BI connects data sources and provides BI reports and dashboards to users. It can connect with just an Excel spreadsheet or bring together cloud-based and on-premises data warehouses. Data pulled from cloud-based sources, such as Salesforce CRM, is automatically refreshed.
With applications such as an Excel workbook and Power BI Desktop file connected to online or on-premises data sources, Power BI users must manually refresh or set up a refresh schedule to ensure Power BI reports and dashboards use the most current data available.
Power BI consists of a collection of apps and can be used on a desktop, as a software as a service (SaaS) product or on a mobile device. Power BI Desktop is the on-premises version, Power BI service is the cloud-based SaaS offering and mobile Power BI runs on mobile devices.
The following are among the different Power BI components that let users create and share business insights in ways that fit their roles:
- Power Query. This data mashup and transformation tool integrates data from multiple sources.
- Power Pivot. This is a memory tabular data modeling tool.
- Power View. This tool lets users create and interact with their own data visualizations.
- Power Map. Power Map is a visualization tool for 3D geospatial data that bolsters predictive analytics.
- Power BI Q&A. This natural language query engine can take user inputs and produce data visualization outputs.
- Power BI Embedded. This tool lets users take customer-facing reports, insights, visuals and other items from Power BI and embed them into other apps or websites.
There are dozens of data sources that connect into Power BI. These include the following:
- Files such as Excel, PDF, SharePoint or XML.
- Databases, including Amazon Redshift, Google BigQuery, IBM databases, Microsoft SQL Server and Oracle Database.
- Other data sets within the Power BI platform can be connected and Microsoft Azure can be integrated with Power BI to serve as a source.
- Online services, including Adobe Analytics, Facebook, Google Analytics, Microsoft Dynamics 365 and Salesforce Reports.
How to use Power BI
Power BI Desktop is where analysts and other users can create data connections, data models and reports. The Power BI service is where those reports can be shared, so other users can view and interact with them.
To build a Power BI report, users must take the following steps:
- Connect their data sources.
- Query the data to create reports based on user needs.
- Publish the report to the Power BI service.
- Share the report, so cloud and mobile users can see and interact with it.
- Add permissions to give or limit colleagues' ability to edit reports and create dashboards.
How much does Power BI cost?
There are three levels of Power BI for users: Power BI Desktop, Power BI Pro and Power BI Premium. The desktop version is free, while the Pro model costs $9.99 per user, per month.
Pricing for Premium depends on the size of the deployment and the number of users. It's split into two tiers: per user and per capacity. The Premium per user tier starts at $20 per user, per month, and the Premium per capacity tier starts at $4,995 per capacity, per month and provides access to Microsoft Fabric, an AI-powered analytics and data management platform.
Power BI vs. Excel
Excel and Power BI are both used to map out data sets and points. However, the two platforms have different uses and levels of in-depth functionality. Both are Microsoft software products that enable visualization and exploration of raw data. Both also enable the creation of reports and interactive dashboards. Power BI, however, is meant to provide more in-depth dashboards and analytics that provide business value and insight from an organization's data. Excel is focused on simpler use cases.
Power BI's visuals and reports are detailed enough to drive actionable insights. The platform analyzes relationships among data points and identifies patterns that drive businesses to act based on these findings. However, businesses still value Excel for its simplicity and other advantages, such as calculating numerical values faster than Power BI.
Power BI use case examples
There are a wide variety of uses for Power BI across different industries. The platform's ability to synthesize data from various sources makes it useful for analyzing and reporting data that's culled using an array of tools and methods. Some of the ways different industry sectors use Power BI to their advantage include the following:
- Healthcare. Patient data is aggregated, synthesized and analyzed to produce reports allowing healthcare providers to make new discoveries or detect new patterns.
- Retail. Reports based on customer purchase data give retailers insight into which products to prioritize and stock.
- Manufacturing and engineering. Power BI dashboards are used for process monitoring and reporting resource use. For instance, manufacturing data collected with IoT devices can be analyzed using Power BI.
- Education. Tracking student performance with Power BI reports and dashboards helps school administrators and teachers identify where improvements are needed.
- Finance and insurance. Power BI is conducive to analyzing the large-scale data sets the financial sector uses. The insurance industry can use reports and dashboards to get insight into risk assessments.
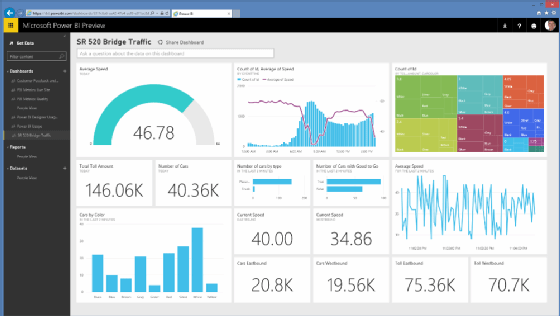
- Public sector. Government agencies use Power BI to analyze intelligence or census data, as just two examples. Local government entities use it as well. Figure 3 shows a custom dashboard on bridge traffic that would be useful for planning transportation development and services.
AI has become common in data analytics, so it's no surprise that generative AI has moved from hype to pragmaticism in this field. Learn about the rise of generative AI in data operations.





